“A Matemática possui não só a verdade…mas também a suprema beleza de uma fria escultura, dona de uma perfeição intrínseca, como só a melhor arte pode mostrar. O verdadeiro espírito de alegria…senso de ser mais que humano…nela se faz presente, ecoando júbilos…de sua inerente Poesia”. (Bertrand Russel – “Mathematics’ Study”)
Durante o século 19 … a matemática: “mãe” reconhecida de todas ciências, começou a voltar sua atenção, a seus próprios fundamentos… No trabalho de Boole, Frege, Morgan, Peano, Russell e outros, um grande projeto aos poucos…começa a ganhar forma: ‘a matemática iria analisar… – com todo o rigor…sua própria estrutura’. O objetivo era um sistema, que fosse inquestionável e seguro. Assim, uma ‘linguagem matemática‘ seria então desenvolvida — com toda clareza…e simplicidade…para dissipar dúvidas, e revelar as suas próprias ‘verdades‘.
O objetivo do projeto era o mesmo sonho de muitos pensadores do século 17 — de criar, ou descobrir uma ‘linguagem universal‘ – na qual um conjunto de símbolos seria usado, para tentar descrever todo ‘conhecimento humano‘…Sua estrutura seria tão ligada à do universo, que a própria… “linguagem“ — por si só — poderia ser usada, para descobrir verdades. Sua sintaxe impediria falsidades…e, não mais haveria significados ambíguos.
Gottfried Wilhelm Leibniz (1646 – 1716) – ao propor uma precisa ‘linguagem simbólica’, era, de fato, uma grande influência sobre a…“sistematização da lógica“…do século 19…e assim criou sua “sintaxe lógico-matemática“. – De fato, sempre houve problemas com o sistema geométrico de Euclides (séc.III a.c.), apesar de sua longevidade. Os 4 primeiros dos 5 axiomas…formadores da ‘geometria plana’…pareciam inquestionáveis… Mas, o 5º axioma (“através de um ponto fora de uma linha…apenas 1 paralela pode ser traçada”), sempre pareceu menos evidente – e por séculos…foram elaboradas inúmeras tentativas de provar sua ‘dispensabilidade’, derivando-o a partir dos outros 4 axiomas euclidianos. Até que foi reconhecido ser impossível tal comprovação – sendo, de fato, independente dos outros axiomas. Esta independência…porém, é intrigante, pois se o 5º axioma fosse contrariado — quando…por exemplo…alguém afirmasse que: “através de um ponto fora de uma linha – nenhuma outra paralela pode ser traçada“…e, se este novo axioma fosse adicionado aos 4 primeiros, os resultados pareceriam…‘absurdos‘. Alguém poderia, por exemplo — encontrar a soma dos ângulos de um triângulo… — maior do que 180 graus.
Desse modo, a descoberta de geometrias não-euclidianas levantou sérias questões — sobre como a matemática deveria ser entendida.
Matemáticos tendem a assumir que termos da matemática… como “ponto“, “linha“, ou “número“, se referem, obviamente a objetos de nossa experiência cotidiana; o que, hoje em dia, já não é tão claro assim… Na verdade, reinterpretando estes termos…poder-se-ia criar sistemas completamente diferentes – alguns dos quais, não tendo nada a ver com a própria experiência… – Como Ernest Nagel…e James Newman … muito bem colocaram:
“É reconhecido que a validade de uma associação matemática, em nenhum sentido depende de significados especiais que sejam associados aos seus termos”… Ou seja: O ‘negócio’ da matemática não é a ‘verdade’; mas sim, sua própria derivação lógica. Mas, se já era difícil…em um campo tão concreto quanto a geometria – determinar quais instruções poderiam ser comprovadas… – e, quais seriam suas contradições; quanto mais difícil isso se tornaria… agora – em sistemas cada vez mais abstratos?

“Não se deve exigir de uma teoria que resolva integralmente, de uma só vez, todas questões pertinentes; basta que ela indique o caminho”. David Hilbert
O avanço abstrato Toda a matemática, foi se tornando mais abstrata no século XIX … já não estando mais “amarrada” a uma descrição do nosso universo… do seu espaço… ou, de seus números. Também desobrigada da confirmação que a experiência tem para dar…como poderia então se ter certeza de que ela … matemática … não estaria criando contradições…nestes ‘reinos sobrenaturais’?
David Hilbert (1862/1943)… que fez mais do que qualquer outro matemático contemporâneo… — no aperfeiçoamento e simplificação dos “fundamentos axiomáticos” da geometria – acreditava que só este método garantiria a ‘segurança‘ de seus resultados.
Para isso – ele propôs uma formalização radical da matemática – ‘todos os sinais matemáticos seriam esvaziados de significado’… Para evitar confusões como as que surgiram na geometria…“demonstrações matemáticas“ não seriam mais do que vestígios de tais sinais, arbitrariamente escolhidos…como “traços“, “hifens” e “letras“. Ademais…’axiomas‘ seriam fragmentos dados pelo sistema…E assim, usando específicas regras mecânicas, tais fragmentos seriam manipulados, para gerar teoremas. A derivação de um teorema … seria apenas uma sequência de fragmentos, organizados de acordo com suas próprias regras…A Matemática seria um jogo de “mecânica sintática“, onde “sistemas metamatemáticos” também estariam aguardando … serem incluídos.
Como podemos determinar se uma dada sequência é um teorema, e sendo, poderia ser comprovado?…Ou então – dada uma interpretação particular do sistema, haveria contradições nele?…Estas questões eram substanciais.
O projeto formalista de Hilbert
Ao tratar “sistemas matemáticos” como de origem puramente sintática, Hilbert chamou atenção às ‘nuances do pensar’, trazendo com isso um rigor abstrato ao propósito de sua “representação ideal“.
Definindo domínios ‘metamatemáticos’ explicitamente — Hilbert logrou assim, levantar ‘questões fundamentais’ sobre ‘verdade‘ e ‘demonstrabilidade‘ no “espírito” da…“ciência matemática“.
Anteriormente, a mais completa tentativa para consolidar a matemática em um sistema havia sido feita por Bertrand Russell e A. Whitehead…em “Princípios Matemáticos” (toda matemática desenvolvida a partir das regras de um cálculo lógico). Para esse caso, Hilbert então perguntou: podemos provar que ele seja ao mesmo tempo consistente e completo…não contenha contradições, e que toda sua afirmação seja verdadeira?
Se uma única aritmética assim formalizada tivesse essas propriedades, este seria o caminho para construirmos uma poderosa ‘linguagem matemática’.
Hilbert reconheceu que, ao realizar esta dupla tarefa – de provar tanto a consistência quanto a integridade, não se poderia apelar para métodos matemáticos comuns, pois eram estes próprios ‘métodos‘…cuja legitimidade estava em questão… – Nem qualquer “evidência” poderia, em ‘metamatemática‘, fazer referência a um número infinito de termos, ou operações… pois tais conjuntos infinitos tinham criado caos e paradoxos na matemática da época… – Respeitando estas restrições…poder-se-ia construir qualquer objeto matemático que se quisesse fazer uso – provando assim sua “existência formal”.

A “Incompletude” de Gödel (1906/1978) “O Teorema da Incompletude é provado pela elaboração de uma afirmação…não provável”.
Mas, como então, Gödel conseguiu – derrubar o projeto de Hilbert?… Ele provou que…sob as restrições de Hilbert, não haveria qualquer evidência de ‘coerência interna’, e que tais poderosos sistemas matemáticos… nunca seriam completos. A ironia é que, demonstrando tal resultado, ele permaneceu nas restrições de Hilbert das “evidências metamatemáticas”.
De fato, a técnica por trás dessa construção é quase tão importante quanto o resultado em si. — Gödel começou com o sistema formal do “Principia Mathematica” — mas… como ele próprio observou – poderia ter escolhido qualquer “sistema formal aritmético“… Em tais sistemas, fatos aritméticos familiares, como “1 + 1 = 2“, seriam representados por signos no sistema… – que poderiam ser manipulados – como se não tivessem significado algum.

O código de Gödel é bem similar ao padrão de criptogramas. Ao codificar letras do alfabeto em nºs poderíamos codificar qualquer tipo de mensagem; e, inversamente…com 1 sequência de nºs codificados… — se decodificáveis, saberíamos então…qual a mensagem.
Tal codificação poderia dividir toda “sequência de nºs” em 2 classes…as “traduzíveis” em mensagens, e as que não poderiam ser decodificadas (ou pelos nºs…não corresponderem às letras codificadas, ou por corresponderem, sem fazer sentido). A ‘codificação de Gödel’ também permitiria caracterizar qualquer número; este seria um Número de Gödel…se, e somente se pudesse ser traduzido em um teorema...ou demonstração no sistema formal. Por outro lado, dado um número de Gödel, poder-se-ia recuperar qualquer sequência.
Tal procedimento pode parecer ridiculamente fútil… – O código é uma interpretação peculiar do sistema formal, que parece… nada mais do que levar os sinais para ainda mais longe dos fatos teóricos – expressos em algarismos básicos… como “1 + 1 = 2“. Porém, como Douglas Hofstadter explica claramente: “A importância da codificação é que o sistema formal então mapeado representa afirmações sobre números“.
Essa técnica é notável em um sistema – a princípio, tão silencioso, quanto a aritmética, mas, dificilmente seria eficaz em uma “linguagem natural”… onde a dificuldade surge a partir de seu ‘poder reflexivo’. Por exemplo, a asserção: “esta afirmação é falsa” é o exemplo clássico. – Sendo falsa…a afirmação é “verdadeira” – por outro lado… se for verdade…então é “falsa“. – Dessa maneira, com seu “código formal”, Gödel criou algo semelhante…uma sequência G, onde, surpreendentemente “G não é demonstrável.”
Com efeito, este não é, num sistema formal um mero paradoxo; G é tanto demonstrável, quanto não… Se é demonstrável, então – considerando sua aritmética consistente – G é verdadeira. Mas G diz que G não é demonstrável…por isso, se fosse verdade, seria falso, e, temos assim uma contradição…G é “não provável”…Mas, isso é exatamente o que diz, por isso é verdadeiro. E assim…temos um ‘exemplo real’ de uma verdadeira declaração, que não pode ser provada… – Seu sistema aritmético…é portanto, “incompleto“.
Além disso, Gödel demonstrou que…“a aritmética é…’essencialmente’ incompleta, não havendo meios de adicionar complementos ao sistema, como axiomas para completá-lo”. Este resultado, em nossa era atual – incerta e relativística… pode não ter o mesmo efeito devastador que teve sobre os matemáticos, que há quase 50 anos, acreditavam que, com axiomas e lógica, poder-se-ia chegar, se não à toda verdade filosófica…ao menos, à mais completa “formalização matemática”. Todavia, a diferença entre “demonstrabilidade” e “verdade”, tem levado a uma ênfase metafórica ainda mais abrangente. – O Teorema de Gödel tem sido utilizado, por exemplo, como argumento que, o ‘mundo natural’ sempre ilude nossas melhores teorias, e assim: “o conhecimento humano nunca alcançará tudo”.

Alan Turing (1912-1954) – ‘máquina de Turing’
‘Limitações computacionais‘ O ‘Teorema de Gödel’ parece sugerir algo bem preciso sobre as limitações dos computadores.
O teorema também tem sido utilizado como fonte de controvérsias na ciência da computação… pois, como diz Hofstadter em seu livro: “Gödel, Escher, Bach… um entrelaçamento de Gênios Brilhantes”: “Sistemas formais … com seu vaivém sintático de sinais e sentidos, são origem de toda computação”.
Em 1936…antes do 1º computador ser construído, Alan Turing criou uma teoria formal de como um computador funcionaria, e hoje tal sistema é visto ao nível mais elementar das máquinas atuais. Bits de informação binária ‘1’ e ‘0’… são manipulados mecanicamente…como leis de inferência de Hilbert manipulam sequências matemáticas.
Hofstadter, em seu comentário sobre um artigo do filósofo J.R. Lucas, contribuiu para um animado debate entre filósofos e cientistas da computação… – Lucas havia escrito: “O teorema de Gödel parece-me provar que a filosofia mecanicista é falsa, isto é, que a ‘mente’…não pode ser explicada – como ‘máquina’…Se a máquina pode ser facilmente programada para criar ‘teoremas’ em certo ‘sistema formal’… – falhará… ao detetar as ‘armadilhas de Gödel‘…latentes nesse sistema – as quais – embora nunca possam ser consideradas como teoremas pela máquina… – ainda assim … podem ser vistas como verdades, pela mente humana. – Por conseguinte… sendo a mente, na verdade…‘viva’, sempre pode fazer melhor do que quaisquer sistemas formais … mortos e ossificados.“

“Os ‘poderes da mente’… excedem os de uma máquina de inferência lógica”. (Michael Polanyi)
Este argumento e outros similares utilizam a demonstração de Gödel para transcender a mente…em relação à máquina; enquanto Hofstadter argumenta de outra forma…Ele acredita que o que vale à máquina também vale ao cérebro … pois ambos são ‘sistemas formais‘. – O cérebro possui um ‘hardware básico‘, composto de… talvez 10 bilhões de neurônios…onde cada um deles – excitado (ou inibido) por sinais característicos, tem a opção de disparar…’neurotransmissores’, de acordo com… ‘rigorosas leis mecânicas‘.
A décadas atrás, em seu clássico livro “Cibernética“, Norbert Wiener escreveu: “O caráter de ‘tudo-ou-nada‘ da descarga do neurônio…é análogo àquela singular escolha a ser feita – quando da definição de um dígito dentro da…escala binária”.
E, se o nível mais elementar do cérebro é também um sistema formal, então deve estar sujeito às limitações do ‘teorema de Gödel‘. Assim, Hofstadter desenvolve convincente argumento matemático de: “por que a mente é tão limitada quanto uma máquina”. No entanto… é um dos temas mais importantes de seu livro que – embora possa haver um sistema formal subjacente a toda atividade mental… — a “mente” — de alguma forma, transcende o “sistema formal” que a suporta. E, sendo o sistema subjacente formal tão poderoso…a ponto de se refletir – mesmo nos níveis mais elementares – então… como assim argumenta Hofstadter… — “uma nova dinâmica … acontece no cérebro”.
Como exemplo, Hofstadter compara o cérebro a uma “colônia de formigas”…que na complexa organização do formigueiro exibe sua estratégia e consciência… enquanto as formigas individuais parecem se identificar aos neurônios… No cérebro, também conjuntos de atividades são formados, e a interpretação se opera quando diferentes níveis começam a interagir. Nesse sentido, Hofstadter oferece mais alguns detalhes:
“Cada aspecto do pensamento…pode ser visto como uma descrição em alto nível do sistema, que a nível elementar é governado por simples regras formais”.
O método de argumento usado na demonstração de Gödel, se torna mais importante, para Hofstadter, do que seu resultado limitador… O uso da verificação de códigos, e seus mapeamentos; sua mistura de níveis; e a vertiginosa ‘recursividade‘, tudo parece levar Hofstadter a implicações metafóricas para a lúdica atividade (de per si) da “inteligência”.
Inteligência artificial… ‘Sem alguma habilidade para se referir à nossa própria atividade mental… e transformá-la… — a “inteligência” seria impossível.’

A mente, escreve Hofstadter, parece agir como as 2 mãos do famoso desenho de Escher, cada uma desenhando a outra. Esse estranho “loop”, afirma ele, pode até ser referência ao próprio processo vital.
Para Hofstadter a mais importante noção encontrada na lógica de Gödel é a “auto-referência“…E ele faz dessa ideia o eixo central de seu texto… numa análise séria, apoiada por – inúmeras ‘alusões lúdicas‘. Esta…é uma das mais ricas e originais de suas “concepções”… – sendo considerada como o processo crucial em nossa mente. Sempre…ao nos corrigirmos…resolvemos “quebra-cabeças“…que nos envolvem em suas interpretações. Hofstadter…em uma de suas metáforas mais ousadas…analisa a transferência de “informações” em uma célula… e, obtém ‘complexidades formais’ da lógica matemática no cérebro humano.
O DNA, por exemplo… contém, ao mesmo tempo…o programa para a atividade da célula; os dados manipulados por enzimas específicas; e o idioma transcrito pelo RNA… sendo…portanto, uma… “cadeia formal“… – interpretada em diferentes níveis.
De fato, todo mecanismo celular…envolvendo a transcrição e tradução do código genético, a partir de uma cadeia do DNA, que indiretamente dirige a sua própria auto-replicação, é mapeado por Hofstadter…em um gráfico elaborado sobre as interpretações e codificações do teorema de Gödel, com sua sequência auto-referente. Com efeito, Hofstadter escolheu o idiossincrático sistema de numeração de Gödel para sua demonstração – e assim…pôde criar uma estreita relação entre esse código… e, o igualmente arbitrário “código genético”, decifrado recentemente… – Dessa maneira então…ele parece querer argumentar… – que:
‘Se a vida pode extrapolar o substrato químico padrão da célula… – e a consciência emergir de um sensível sistema de neurônios… – então… os computadores também podem alcançar o nível da inteligência humana’.
E – na verdade – de forma rudimentar…sistemas formais elementares do computador já correspondem às… “complexidades da inteligência”… (talvez… por terem sido projetados também de forma inteligente). Sequências básicas binárias de informação são agrupadas em “palavras“…e interpretadas de diversas maneiras…como nºs, endereços, e comandos. Linguagens de informática em alto nível…praticamente eliminam o “ruído eletrônico“, agrupando em padrões, as transferências mecânicas de bits de informação, se ajustando, eventualmente … à experiência cotidiana do programador – como reconhece Hofstadter: “Há um longo caminho a percorrer – mas… eventualmente… – um computador poderá ser programado para se tornar indistinguível da mente humana”. E realmente este não é um sonho impossível… a ‘inteligência artificial’ já é um importante campo de pesquisa.
Margaret Boden, em seu recente trabalho, ‘Artificial Intelligence and Natural Man’, transmite a enorme emoção, e teimosa perseverança dos pesquisadores da área. Muito já foi alcançado… – há programas para o jogo de damas…aprendizado de línguas, etc. Estes são indícios de uma “inteligência universal”… mas Hofstadter é deveras persuasivo sobre potencialidades da…”Inteligência Artificial”…ao menos em seus insights sobre processos envolvidos na resolução de problemas. – Na verdade… ele não só quer discutir o assunto em suas várias formas (demonstração de Gödel, Inteligência Artificial, células, etc.) mas, criá-lo no texto, como um “modelo literário”, em um grande “ciclo auto–referencial“.

Jogos lúdicos (Escher & Magritte)
Muito do que está por vir … com efeito, também tem a ver com Escher… Seus desenhos…na maior parte, são truques divertidos explorando auto-referências níveis de interação, jogos de fundo, etc. intrigantes, instigantes…e às vezes, até inquietantes… ‘truques proposicionais’ de formas de imagem…Como analogia, muitas das ideias do autor, confundem visões profundas… às mais superficiais, como a figura de fundo de um desenho, ou meta-sistemas regulares/aleatórios.
Uma implicação do teorema de Gödel porém…é que em certos sistemas formais… “figura e fundo não carregam a mesma informação“.
Ao se entregar a uma consideração metafórica do conhecido teorema lógico de Alfred Tarski (1901-1983)… que afirma — “não existe um critério mecânico para determinar a verdade das afirmações de certos sistemas matemáticos… – incluindo a aritmética”, Hofstadter diz, do mesmo modo: “não haver procedimento decisório para beleza na arte”…sugerindo…para tanto… – alguma “remota ligação” com o Teorema de Tarski. Contudo, essas referências se tornam um problema sério – pois seu livro se preocupa diretamente com a natureza das relações – ou “traçados“…entre os sistemas formais.
Hofstadter, em suas discussões sobre Gödel… cérebro… computadores… e células, utiliza vários “dispositivos formais” para ‘conectar’ os sistemas tratados… textos e ideias reduzem-se à sintaxe…enquanto mapas/gráficos distinguem variedades de objetos… por sua forma compartilhada. – Tal identificação … acredita Hofstadter, contém significados sugestivos — em uma correspondência… do “sistema auto-referencial” de Gödel … com o próprio “código auto-replicador” das células.
“Formalismos analógicos” devem ser preenchidos com interpretações – antes de espontaneamente delineados. A dificuldade então, não reside em criar ‘paralelos formais’…mas em produzir interpretações de julgamento…não na ‘sintaxe‘, mas, ‘semântica‘. Hofstadter discute trocas de significado e limitações formais. Muito embora costume falar sobre as complexidades da linguagem … fica mais à vontade ao expor formalismos. Aceita, por exemplo, o proposicional das artes de Escher e Magritte – por ‘ilustrarem’ suas noções sobre níveis… e auto-referência.
Estabelecendo correspondências que envolvem ‘recursividade‘… entre a teoria de Gödel, a célula, e a mente…Hofstadter tenta provar certa transcendência, ao revelar estruturas semelhantes – mostrando que – o que se mantém em um sistema…pode também acontecer em outro. – Para ele, consequências ‘imprevisíveis‘ podem estar em jogo. — Quando sistemas formais alcançam certo nível de “complexidade”… – a sequência de Gödel pode se reproduzir … a vida surgir … e a inteligência ser criada. Porém, essas correspondências são inconclusas e metafóricas … mais assertivas, do que convincentes. Para mostrar como poderiam alcançar criatividade … Hofstadter teria de, por conta própria, articular uma ‘teoria do significado’. Ele teria que se deslocar…dos sintáticos…estruturais…e formais ‘vínculos’ … de diferentes valores e profundidade…para uma visão puramente…”semântica“…da linguagem… e da arte.
O que a tartaruga disse para Aquiles… “Bem, agora, você gostaria de ouvir a estória de uma pista de corridas, onde as pessoas imaginam poder chegar ao fim em 2 ou 3 passos…mas, que na verdade são um número infinito de distâncias?” (Lewis Carroll)
O diálogo de Lewis Carroll, que Hofstadter toma como modelo é uma brilhante analogia lógica ao paradoxo de Zenão, de como a tartaruga mostra o que Aquiles nunca resolverá com a ajuda de um silogismo (raciocínio dedutivo)…“Se A e B são verdade, então Z deve ser verdadeiro”. A tartaruga não aceita Z, mas há ainda outra proposição D que ela deve aceitar…”Se A, B e C são verdadeiras, então Z deve ser verdadeira”… e assim por diante.
O paradoxo de “Aquiles e a tartaruga”, proposto por Zenão, por volta de 450 a.c. – retrata uma situação hipotética entre dois personagens, onde… numa corrida entre eles… — Aquiles ‘nunca’ alcançaria a tartaruga – pois, mesmo a velocidade maior — estaria sempre, se aproximando dela… — Isso ocorre porque… depois de cobrir a distância, que então, os separava – terá sempre mais uma fração … da nova distância entre eles…a ser então…percorrida; e assim por diante… – “ad infinitum“.
“Aquiles não pode dar um número infinito de saltos para alcançar a tartaruga … porque não existem saltos infinitamente pequenos, em um espaço… feito de grãos de tamanho finito”. (Carlo Rovelli)
A questão da ‘regressão infinita contínua’, nos lembra uma questão de Wittgenstein: “Por que seríamos obrigados a ter de aceitar alguma conclusão lógica?”…Hofstadter responderia que há sempre um…‘substrato inviolável’…na célula…na mente…no computador…“um sistema formal que é o limite da regressão infinita … fim de toda procura – para se chegar ao conhecimento fundamental”. Contudo…a princípio não vejo razão para aceitarmos esta solução. – Problemas lógicos de “regressão infinita” não são resolvidos, tendo como referência um “hardware”… – “Você não pode ir em defesa de seus padrões de raciocínio para sempre, pois acaba chegando a um ‘ponto crítico’ onde, inevitavelmente, a fé assume o controle” (assim explicaria Hofstadter).
Hofstadter, tal como Hilbert, tem fé que a ‘Inteligência Artificial’ terá sucesso; ainda mais, porque acreditava que… para o sucesso do programa ‘A.I‘… não deveria existir obstáculos comparáveis ao que bloqueou Hilbert – entretanto…não há qualquer evidência sobre isso. Hofstadter não minimiza as dificuldades, mas as chances parecem formidáveis. O cérebro em si parece mais um sistema probabilístico…que formal – mais uma nuvem…do que um relógio (usando a metáfora de Popper)…e, por sua interação com o resto do corpo…seria também muito difícil considerá-lo um sistema independente de um “desempenho global”.
Pesquisadores em AI esperam nunca ter de modelar a fisiologia do cérebro; eles se concentram sobre o funcionamento da mente, e tentam imitar suas características. Todavia, mesmo esse simples projeto, já parece enorme. A realização do programa significaria um conjunto finito de instruções fornecendo uma verdadeira estrutura da mente humana… – uma sequência de proposições – em que se poderia ler uma “gramática universal da criatividade“… — Tal projeto é o ‘sonho arquétipo’ de grande parte da investigação contemporânea… Sua finalidade, não é encontrar uma ‘linguagem universal’…cuja sintaxe revelasse a “verdade do mundo”… (Gödel provou ser isso impossível) mas uma interpretação universal, que reduzida a uma sintaxe subjacente de estruturas básicas…explicasse a complexidade a nossa volta.
Livre Tradução (“resumo”) da resenha de Edward Rothstein para o livro de Douglas Hofstadter… ”Gödel, Escher, Bach: um entrelaçamento de Gênios Brilhantes” ‘The Dream of Mind and Machine’ (dez/1979) consulta…K. Gödel & D. Hofstatder ******************************************************************************
“Teoremas da Incompletude” “Como um sistema matemático não pode provar a sua própria consistência interna, nem ser usado para provar a consistência de outros… – é sempre possível definir proposições que não podem ser testadas em função dos axiomas que definem este sistema…Portanto, sempre haverá declarações formais verdadeiras… – que o sistema jamais poderá provar”.
- Teorema 1: “Se o conjunto axiomático de um sistema formal é ‘consistente‘, então nele existem teoremas, que não podem ser demonstrados… ou negados”.
- Teorema 2: “Não existe qualquer teoria, cujo ‘procedimento construtivo‘ seja capaz de demonstrar por seus próprios meios, sua própria consistência“.
(“incompletude”)…Qualquer “sistema lógico” … de qualquer ‘complexidade’, contém mais proposições verdadeiras do que pode ser provado… – por seus próprios axiomas…Daí então resulta:
(consistência interna) que … “sistemas axiomáticos aritméticos”, por exemplo, só podem ser provados… — por outros sistemas axiomáticos … (semelhantes).
Paradoxo de Liar — a afirmação… “Esta sentença é falsa!” é uma proposição indecidível…(tanto falsa quanto verdadeira)
A matemática possui 3 classes de sistemas: a) discretos – associados aos nºs naturais; b) contínuos – associados aos nºs reais; c) fractais – associados aos sistemas caóticos.
Sistemas Caóticos (não-lineares)
A turbulência em um sistema dissipativo é um movimento caótico induzido a desenvolver certo padrão. Este padrão – que varia para cada fenômeno físico, é denominado “estranho atrator“…Este nome se deve ao fato de tais sistemas serem atraídos a um destino ‘bem definido’… – assim como “sistemas lineares” tendem a pontos fixos, ou ciclos. Porém, diferente destes, os ‘atratores’ não são pontos, ou curvas bem definidas — mas sim…‘objetos caóticos‘…de natureza (geométrica) fractal… – com ‘dimensões não-inteiras’… Sendo extremamente sensíveis às condições iniciais…revelam um contínuo de frequências… ao invés de frequências aleatórias… similar ao de sistemas não-lineares. (Michel Janos) ************************************************************************
 “Prova de Gödel” (o livro) Matheus Martins Silva
“Prova de Gödel” (o livro) Matheus Martins Silva
Este livro introduz o leitor … a uma das descobertas mais importantes do século 20: os “teoremas da incompletude” de Gödel. Em 1931, Kurt Gödel, jovem matemático de 25 anos…publicou num periódico alemão o artigo intitulado “Das proposições indecidíveis de principios matemáticos e Sistemas Correlatos”. — As conclusões contidas em tal artigo são um ‘divisor de águas’ na história da lógica e da matemática — sistemas dedutivos como a aritmética não podem ser completamente axiomatizados – e, quaisquer métodos que utilizemos para demonstrar a ‘consistência‘ desses sistemas serão tão complexos – que sua coerência fica tão aberta a dúvidas, quanto a dos próprios sistemas.
Em 8 capítulos de prosa clara e rigor conceitual, Ernest Nagel e James Newman narram o percurso histórico que levaria à prova de Gödel. À medida que novas áreas da matemática foram dotadas com conjuntos de axiomas…surge, no século 19…a esperança de que toda a matemática poderia ser dotada de um ‘conjunto de axiomas‘. — Se fosse possível fornecer uma axiomatização completa da ‘aritmética‘…axiomatizar as demais áreas da matemática seria apenas questão de tempo. Tanto os ‘Principia’ de Russell…como a ‘metamatemática‘ de Hilbert são exemplos desses modelos axiomáticos, que tinham como objetivo fornecer uma prova dessa aritmética…Essa esperança “caiu por terra” com as conclusões de Gödel.
Para ilustrar o assunto — tomemos como exemplo a “metamatemática” de Hilbert. Seu significado pode ser assim definido: “A matemática constitui os sistemas formais estudados pelos matemáticos; a “metamatemática” é a teoria acerca desses sistemas”. Expressões que ocorrem na matemática…devem ser compreendidas como isentas de sentido, o que importa são suas estruturas e o modo como se combinam. Expressões que ocorrem na metamatemática, por outro lado, são “significativas”…sendo a partir delas que iremos avaliar se a aritmética é consistente… – demonstrar que 2 fórmulas contraditórias não podem ser ambas derivadas dos axiomas da aritmética, quer dizer que a aritmética é consistente. Mas Gödel demonstrou aí…2 obstáculos insuperáveis.
O 1º obstáculo é demonstrado pelo “Primeiro Teorema da Incompletude” (prova da existência de “proposições indecidíveis” no cálculo dos “Principia Mathematica“…e sistemas semelhantes)…em qualquer ‘sistema axiomático’ – suficientemente amplo para expressar a aritmética, é possível construir uma fórmula aritmética verdadeira F que é exprimível no sistema, mas não demonstrável nele. – Tais fórmulas têm um correspondente enunciado metamatemático afirmando sua própria “falsidade”, isto é, F diz de si própria que é indemonstrável. – Sendo F demonstrável, então F é uma verdade aritmética. Por outro lado, ao afirmar ser ela própria (F) não demonstrável, sua demonstração implica a sua falsidade. Mas se a aritmética admite uma fórmula, e sua negação como verdades, então é inconsistente. Portanto F é verdadeira, e não pode ser demonstrada por uma axiomatização da aritmética – pois se F pudesse ser demonstrada nesta axiomatização teríamos uma contradição. Logo F é ‘indecidível‘.
Como consequência, a ‘axiomatização’ da aritmética apenas poderá ser consistente se for inerentemente incompleta…e, só poderá ser completa, se for inconsistente. Qualquer axiomatização consistente da aritmética é incapaz de abranger todas as “verdades” da aritmética… — portanto, uns sistemas podem abarcar mais verdades que outros – mas nenhum deles pode ser capaz… — de abranger todas as verdades da aritmética.
 O 2º obstáculo ‘insuperável’…é demonstrado pelo 2º ‘Teorema da Incompletude’ de Gödel, um corolário do 1º (é impossível provar – no cálculo do Principia Mathematica e sistemas similares, a consistência do próprio sistema): Nesse sentido, a consistência de um ‘sistema axiomático’ – suficientemente amplo … para conter em si toda a aritmética…não pode ser demonstrada no interior deste próprio sistema. Se a axiomatização da aritmética proposta por Hilbert for consistente, o enunciado ‘metamatemático‘ – que representa a sua própria consistência, não é demonstrável nessa axiomatização. A consistência de sistemas como a metamatemática de Hilbert somente pode ser demonstrada com o emprego de ‘princípios’ logicamente mais complexos…que os próprios princípios da ‘metamatemática‘ de Hilbert.
O 2º obstáculo ‘insuperável’…é demonstrado pelo 2º ‘Teorema da Incompletude’ de Gödel, um corolário do 1º (é impossível provar – no cálculo do Principia Mathematica e sistemas similares, a consistência do próprio sistema): Nesse sentido, a consistência de um ‘sistema axiomático’ – suficientemente amplo … para conter em si toda a aritmética…não pode ser demonstrada no interior deste próprio sistema. Se a axiomatização da aritmética proposta por Hilbert for consistente, o enunciado ‘metamatemático‘ – que representa a sua própria consistência, não é demonstrável nessa axiomatização. A consistência de sistemas como a metamatemática de Hilbert somente pode ser demonstrada com o emprego de ‘princípios’ logicamente mais complexos…que os próprios princípios da ‘metamatemática‘ de Hilbert.
As descobertas de Gödel têm grande importância, mas ainda não foi totalmente compreendida a extensão do seu alcance. Uma das razões dessa incompreensão é terem sido tão deturpadas por interpretações inconsequentes – que se tornou difícil perceber sua real significância. O desfile dessas interpretações vai, desde filósofos pós-modernos, que veem nisso o surgimento de uma nova ciência; até ‘irracionalistas’ – para quem tais conclusões são uma derrota da “lógica formal”. Mas… na verdade – os achados de Gödel não têm nenhuma destas implicações, considerando que o próprio Gödel comprovou a consistência da ‘lógica clássica’: “The Completeness of the Axioms of the Functional Calculus of Logic”, de 1930.
Uma consequência real dentre várias que podemos inferir das descobertas de Gödel, é que a verdade matemática não pode ser identificada com a dedutibilidade, a partir de axiomas, ou meras convenções linguísticas. Esse resultado então inviabiliza uma “epistemologia positivista”… — a qual buscava explicar o… “conhecimento a priori“, reduzindo-o ao mero conhecimento linguístico. O último “teorema de Fermat“…por exemplo, permaneceu como uma conjectura durante séculos, até sua demonstração no século 20. – As justificativas “racionalistas” são inevitáveis nesse caso…pois não podemos esgotar tal ‘verdade matemática’ em ‘convenções linguísticas’…Uma outra consequência é que aquilo que denominamos de ‘prova matemática’ nada tem a ver com método axiomático formal, pois os axiomas e regras de demonstração, fixados inicialmente – não poderiam impor um limite à inventividade dos matemáticos, na criação de novas demonstrações – tudo ainda conforme ‘justificativas racionalistas’.
O livro de Nagel e Newman procura explicar a estrutura básica das demonstrações de Gödel de modo acessível…sem perder a tecnicidade necessária nessas demonstrações. Outro mérito do livro é dar instrumentos conceituais necessários a esta compreensão: noções fundamentais como axioma, teorema, modelo, consistência…entre outras, são adequadamente vistas…a cada capítulo. Sendo das melhores introduções disponíveis às descobertas de Gödel, o livro segue sendo reeditado desde 1958. (texto base 2008) ******************************************************************************
Uma viagem informal ao Teorema de GÖDEL (Ricardo S. Kubrusly – IM/UFRJ) “O teorema de Gödel é o mais surpreendente…o mais comentado, e com certeza, o mais incompreendido resultado matemático do século passado…e do que começou a chegar”.
É interessante observar as semelhanças entre matemática e outros conhecimentos mais, digamos, maleáveis, que este famoso teorema permite estabelecer…É raro ver o cidadão educado curioso a respeito de algum teorema matemático… Nem mesmo o famosíssimo ‘último teorema de Fermat‘ que por mais de 300 anos desafiou talento e engenhosidade do raciocínio abstrato da humanidade, desperta – a não ser entre os especialistas, tanta curiosidade e suscita tanta fantasia quanto os resultados do “teorema da incompletude”. Pretendemos visitar a prova do “teorema de Gödel”…numa tentativa de apresentar e discutir suas principais ideias e consequências, para a matemática, e para a sociedade.

Três Paradoxos … em análise (M. Escher “smaller and smaller”)
A tentativa de diluir a contradição dos “paradoxos”, por sentenças matemáticas corretas… — acaba nos levando a várias versões do… abismo… — onde o “panorama aconchegante” erigido — nos devolve a esperança por um ‘mundo matemático’ verdadeiro, livre de suas infindáveis contradições… — no qual, apenas “apreciações fidedignas” seriam reveladas.
a) paradoxo do barbeiro: Diz-se que em Sevilha havia um barbeiro que na porta de sua casa pendurou uma tabuleta com os dizeres: “Faço a barba de todas e somente das pessoas que não fazem a sua própria barba”. A pergunta: “Quem faz a barba do barbeiro?” nos leva ao ciclo auto-contraditório dos paradoxos. – Se o barbeiro faz a própria barba, como ele só faz a barba daqueles que não fazem a própria barba… – então…ele não faz a própria barba, mas neste caso, como ele não faz a própria barba… e como ele faz a barba de todos aqueles que não fazem a própria barba, então ele faz (e não faz)…paradoxalmente, a própria barba.
b) paradoxo de Russell – transporta irrefutavelmente para o campo da lógica formal e da teoria dos conjuntos…o convívio promíscuo do falso e verdadeiro. – Podemos imaginar que todas as coisas que existam…pertençam a uma – entre duas classes de objetos: as das que contém a si mesmas (como por exemplo a classe das ‘coisas imagináveis’, que em si, é uma coisa imaginável) … e as das que não contém a si mesma (como por exemplo a classe dos vegetais ou dos matemáticos, que em si própria, não é nem vegetal, nem matemático).
Chamando a esta última de “normal” e a primeira de “anormal”, e designando por N o conjunto de todas classes normais, pergunta-se: será N normal?…Bem, se N é normal, então N pertence a si mesma (pois N é o conjunto de todas as classes normais) mas se assim for, pela definição de anormal, N é anormal… e então, N não mais pertence a si mesma…e conseqüentemente é. — Ou seja: N é normal…se e somente se N é anormal. O “paradoxo de Russel“ baseia-se apenas na noção de classe de conjuntos…dentro da precisão da lógica. Aceitando a noção de ‘classe’, ele fica definitivamente estabelecido.
c) paradoxo de Richard – elabora a mesma ideia do de Russell, mas traz para dentro do âmbito matemático, a angústia do paradoxo, mapeando a auto-contradição dentro da aritmética, fazendo transportar, inesperada e inexoravelmente – para a estrutura lógico-matemática…o perigo da inconsistência – que é expressa pela existência da ‘contradição’.
Considere uma linguagem onde “propriedades particulares” aos nºs sejam definidas…lógico que não podemos ir ‘definindo tudo’, mas, começar de onde já houver um prévio entendimento…onde alguns termos aritméticos serão presumivelmente, considerados então…por nosso entendimento, como fazendo…”pleno sentido“.
A propriedade de ser “número primo“…seria definida como ‘divisível apenas por si mesmo, e pela unidade‘, ou a de ser um número par, como ‘múltiplo de dois‘, etc. Com cada uma das definições arrumadas em série…numa lista ordenada de propriedades aritméticas, associaremos ao seu 1º elemento o nº 1… ao 2º elemento da lista o nº 2… etc. Como cada definição ficará associada – a um ‘único’ número inteiro – pode acontecer em certos casos, que o próprio nº associado a certa definição, por acaso, tenha a propriedade descrita por ela própria. Por exemplo…se considerarmos o nº 19 associado à definição da propriedade de um ‘nº primo‘ (“divisível apenas por si mesmo e pela unidade”) — esta é uma relação verdadeira. Por outro lado, é mais provável acontecer o contrário … que o nº associado à definição de uma certa…”propriedade aritmética”…não possua a propriedade descrita pela definição a ele referida. — Por exemplo… se o número associado à definição da propriedade de um número par é 35, fica evidente que ele não possui esta propriedade.
Os números que se referem aos casos descritos no segundo exemplo…serão chamados de Richardianos; assim, um nº será Richardiano se ele não possuir a propriedade aritmética descrita na definição associada a ele…numa lista confeccionada de definições aritméticas. Caso contrário, serão “NÃO Richardianos” – isto é, quando possuirem a propriedade por ele designada na lista de definições das propriedades aritméticas. – A propriedade de ser Richardiano passa a ser uma “propriedade aritmética” dos números inteiros…e portanto, também terá a ela associado um número inteiro (N). – E assim, repetindo a pergunta do paradoxo de Russell “Será N Richardiano?”…mais uma vez estamos diante da antinomia:
N É Richardiano se e somente se N não é Richardiano.
Aparentemente, conseguimos construir um paradoxo dentro da aritmética…pois toda a argumentação é reduzida a números. Mas a verdade não é bem essa. Ao estabelecermos as regras para a listagem enumerada das propriedade aritméticas dos números — que é usada na construção de “Richard“, nos comprometemos, pelo menos implicitamente, a listar apenas propriedades aritméticas pertencentes estritamente à matemática, e não à “metamatemática“… – conjunto das afirmações a respeito de sentenças estritamente matemáticas. Porém…a propriedade de ser ou não Richardiano não é uma propriedade estritamente aritmética, pois julga a condição de um dado número natural referente ao enunciado de uma lista construída artificialmente. Não é, de modo algum, propriedade inerente ao número. E essa “promiscuidade“ entre matemática e metamatemática…em última análise, possibilita a construção do paradoxo. – Não há trapaças, mas falta rigor.
O Problema da “Consistência” Uma matemática consistente … é livre de paradoxos. O perigo das contradições vai além do que podemos, a priori, imaginar.
Uma matemática consistente é uma matemática…livre de contradições…O que esperamos depois de mais de 6 mil anos de razão, coragem e paciência…é que, ao articular “verdades auto-evidentes” descritas em postulados, não deixemos tais verdades cair em contradição. Para isso então devemos evitar todo tipo de paradoxos. Por outro lado, é possível mostrar que em um “sistema lógico formal“…onde se é capaz de demonstrar uma afirmação e seu contrário … tudo é dedutível. – Em outras palavras, para nos livrarmos dos paradoxos…e provarmos a consistência de um sistema – é preciso encontrar uma afirmação que não possa ser provada dentro do sistema. – Mas…Qual?…Como?… – O que é isso?
Estamos no final do século 19, o sucesso das matemáticas do século 18 levou à certeza do triunfo absoluto da razão. – A matemática era capaz de seguir…e, até mesmo de prever a natureza. Tamanho era o seu poder, inclusive do ponto de vista prático que possibilitava, e ainda possibilita ao homem, construir um progresso modelado ao seu capricho… Já do ponto de vista abstrato, com a análise criteriosa do infinito passa a delimitar ambições e expectativas da própria criação…Cabia então agora, a prova final do que já todos tinham, havia tanto tempo, certeza…de que a matemática era livre de contradições. E logo agora que surgiam como ‘pragas’ … gerados talvez pelo abuso e irreverência com que se lidava com o infinito, paradoxos carregados de contradições, de todos os lados…Mas a situação estava sob controle. – Pelo menos… na mente dos melhores cérebros… que trabalhavam unidos e convictos da possibilidade de livrar a matemática de todo e qualquer paradoxo.
A história que vai desta época ao início da década de 1930 é fascinante, e tem sido contada e recontada de maneira brilhante por muitos autores. Mas por ora, iremos direto aos fatos que levaram à prova do “Teorema de Gödel”… Neste contexto, verdades e falsidades serão sempre tomadas como relativas aos fundamentos do sistema considerado, e assim, dentro da matemática, relacionar-se-ão aos postulados iniciais … que definem sua axiomatização.
Mesmo assim, um conceito de falso ou verdadeiro poderá ser estabelecido fora do sistema – por valores outros, que não os inerentes à formalização que se analisa. Serão afirmações meta-sistemáticas que…a princípio, não interferirão no sistema — a não ser … quando por ele próprio solicitadas.
princípio do terceiro excluído. Este princípio estabelece que uma afirmação P num sistema lógico formal é “ou verdadeira ou falsa“… não podendo portanto ser “falsa e verdadeira”, nem tão pouco “nem falsa nem verdadeira” . Estas 2 proibições constituem em si mesmas o ‘3º excluído’, delimitando o espaço lógico das matemáticas tradicionais. A existência dos paradoxos com sua “dinâmica contraditória”… é fruto deste princípio.
 “Esta afirmação é falsa“, ou qualquer um dos nossas antinomias favoritas – só constituem ‘paradoxos‘ por não ser dada a possibilidade delas serem…nem falsas, nem verdadeiras, ou falsas e verdadeiras ao mesmo tempo… Admitindo o 1º caso: nem falso nem verdadeiro, o caráter contraditório, se tornaria… “indecidível“.
“Esta afirmação é falsa“, ou qualquer um dos nossas antinomias favoritas – só constituem ‘paradoxos‘ por não ser dada a possibilidade delas serem…nem falsas, nem verdadeiras, ou falsas e verdadeiras ao mesmo tempo… Admitindo o 1º caso: nem falso nem verdadeiro, o caráter contraditório, se tornaria… “indecidível“.
Com os paradoxos remetidos para fora do sistema, seria então impossível decidir sobre a “veracidade” ou “falsidade” da afirmação. – O preço de nos livrarmos dos paradoxos seria o reconhecimento, por parte do próprio sistema…de seus limites.
Há afirmações geradas dentro do próprio sistema, sobre as quais este não tem competência para opinar… Já no 2º caso, admitindo desta vez a possibilidade do falso e verdadeiro — incorporaríamos as contradições … dentro do sistema. Paradoxos não mais seriam sintomas de seu mal funcionamento – todavia…o sistema não mais decidiria sobre as verdades e falsidades de suas afirmações.
As soluções da lógica. Se o paradoxo é o problema que devemos evitar, podemos atacar diretamente na lógica…Basta substituirmos a dupla proibição do princípio do 3º excluído … por uma de suas 2 possíveis negações.
A lógica paraconsistente. Quando substituímos a dupla proibição do princípio do terceiro excluído apenas pela segunda delas, relaxando a proibição de uma afirmação ser “falsa e verdadeira“…mas mantendo o impedimento quanto à possibilidade de uma afirmação vir a ser… “nem falsa nem verdadeira” – obtemos a chamada “Lógica paraconsistente“, lugar onde as contradições podem existir e ser articuladas…e, onde não há o desejo imperativo da consistência. É a lógica possível aos paradoxos e talvez, a mais adequada para modelar a “complexidade do homem”, aos limites da sua razão.
A lógica paracompleta. Se desta vez mantemos a proibição da possibilidade de ‘falso e verdadeiro’, mas permitindo surgir uma 3ª via “nem falso nem verdadeiro“, obtemos a ‘lógica paracompleta’, onde não há esperanças de que verdades surjam para dar sentido. Aqui, nem Deus nem Dante existirão pela simples impossibilidade de viver sem eles. Não há provas por contradição pois não há contradições, só indecidíveis. Tal lógica sustenta a uma “matemática intuicionista”…que busca na natureza resposta a suas básicas questões.
O indecidível e a matemática. Embora tentados pela ‘matemática intuicionista’, que nos livraria do problema qualificando-o como não existente, nos livrando desta maneira do sintoma do paradoxo … optamos por uma outra abordagem. – Queremos preservar a potência e a vastidão de resultados que a matemática fundada na ‘teoria cantoriana‘ dos conjuntos nos legou, e resolvemos descobrir os verdadeiros limites deste modelo e desta opção. Paradoxos indicarão o limite dos nossos sistemas se não quisermos contradições.
Há que evitá-los…E, como fazê-lo?…Com seus teoremas…Gödel demonstra que: “a aparição de paradoxos na matemática é inevitável”. — Então… para manter a “consistência” desejada, temos de expulsá-los, reconhecendo…em um sistema – suas próprias limitações de não saber julgar … se verdadeiro ou falso, as ambíguas afirmações veiculadas dentro destes paradoxos … “indecidíveis“.
O preço de consistência é a existência de indecidíveis Para discutir matemática, precisamos de uma linguagem…e um conjunto de regras a serem seguidas. Na década de 1930, Gödel provou que, independentemente de como selecionamos nossa linguagem, nela sempre haverá afirmações verdadeiras, que não podem ser provadas a partir de seus axiomas iniciais. Surge aí…um dilema filosófico: “O que é uma afirmação verdadeira se você não podemos justificá-la?”…Desse modo, nos tornamos então limitados…naquilo tudo que podemos fazer. (Andrew Granville)
A afirmação indecidível no sistema matemático não pode ser avaliada como falsa ou verdadeira, dentro do próprio sistema, mas só por um agente exterior. Chamaremos de “Metamatemática” o conjunto das articulações sobre os conceitos da matemática, propriamente ditos. Assim as fórmulas “0=1” ou “5=2+3” pertencem a matemática, todavia, as afirmações “a equação ‘0=1‘é falsa” ou “a equação ‘5=2+3‘ é verdadeira” pertencem a metamatemática. Outrossim, na construção do “paradoxo de Richard“, as propriedades de um dado número inteiro ser ou não…primo, ou múltiplo de 2…é uma propriedade de aritmética – e, portanto… pertence à matemática – enquanto a propriedade de um dado número ser ou não…’richardiano’ – já não pertence mais à matemática…pois não é uma propriedade própria do número em si, mas sim de sua posição relativa — a uma lista artificialmente construída — como já antes explicado.
Considerando a afirmação matemática P… “P pode ser (ou não ser) demonstrada” também pertence a “metamatemática“, muito embora a sua prova ou contraprova sejam da alçada da matemática. Apenas a “metamatemática” poderá opinar sobre a verdade ou falsidade de um “indecidível”…opinião sempre baseada numa lógica mais abrangente e menos restritiva, do que a adotada para o sistema matemático.
“A Prova de Gödel” A matemática, dentro dos domínios de sua linguagem imparcial, é o lugar da articulação lógica por excelência, tendo sido desenvolvida com tal finalidade; sendo justamente esta… – a verdadeira razão do seu… “retumbante sucesso”.
Há uma grande diferença entre um raciocínio cotidiano, usando a linguagem corrente como veículo e um…”raciocínio codificado” – numa linguagem a mais isenta possível, como o que se dá na ‘matemática’. — Esta diferença não é qualitativa ou quantitativa…do ponto de vista da ‘expectativa’ do raciocínio. — O lugar para onde a ideia nos leva — independe de como a veiculamos – sempre quando… – imparciais, seguimos…‘regras lógicas‘…pré estabelecidas.
A questão não é saber se iremos mais ou menos longe (…certamente menos) com ela, mas criarmos condições de caminharmos com menos medo. Se, e aonde conseguirmos chegar, estaremos confiantes de lá termos chegado, sem sermos conduzidos pelas mãos da ilusão. A matemática não tem o poder imaginado no final do século 19 … mas ainda proporciona um caminhar seguro pelos labirintos espirais do conhecimento. Será possível reconstruir a estratégia da conquista dessa consistência dentro da própria matemática? Será possível encontrar… – não obstante premissa anterior, uma afirmação que não possa ser provada dentro desse próprio sistema?…Com efeito, Esta é a epopeia descrita pela prova de Gödel.
Para começar, a ideia básica é a de mapear toda a matemática para dentro da aritmética. Com isso, qualquer questão aritmética fica reduzida à sua contrapartida aritmética. Esta, por sua vez, é escolhida por ser o ramo da matemática onde se sofre menos interferência da intuição e do desejo. Nela, não há desenhos nem analogias com a natureza para guiar o raciocínio…que passa a se valer apenas de possíveis inserções lógicas. Este trabalho de mapeamento foi resolvido por Hilbert no início deste século…mas Gödel também queria mapear a “metamatemática” para dentro da ‘aritmética’…para assim poder classificar as afirmações acerca dos resultados matemáticos. Com isso, evitaria a tal “promiscuidade“ entre matemática e metamatemática (evidente no paradoxo de Richard), contornando o que restava de trapaça na construção dos paradoxos. – Com essa finalidade… criou uma numeração que leva o seu nome – e que, em si… – é um feito de grande engenhosidade.
O número de Gödel. Para criar uma linguagem estritamente numérica capaz de descrever e articular os resultados matemáticos…Gödel construiu um sistema que associa a cada “símbolo“ (usado na escrita matemática) um único número natural. Passa então a numerar todas as ‘fórmulas’ e ‘considerações metamatemáticas’ que necessita para lidar com os paradoxos. – A numeração segue a seguinte estratégia:
| Sinais | Número de Gödel | Significado |
| ~ | 1 | não |
| v | 2 | ou |
| -> | 3 | implica |
| ∃ | 4 | existe |
| = | 5 | igual |
| 0 | 6 | zero |
| s | 7 | sucessor |
| ( | 8 | pontuação |
| ) | 9 | pontuação |
| , | 10 | pontuação |
Além destes símbolos básicos… — Gödel prossegue a sua numeração, associando os nºs primos maiores que 10 às variáveis independentes:
| Variável | Número de Gödel |
| x | 11 |
| y | 13 |
| z | 17 |
As fórmulas matemáticas seriam numerada… pelos quadrados dos números primos maiores do que 10:
| Fórmulas | Número de Gödel |
| p | 11² |
| q | 13² |
| r | 17² |
Tais propriedades também poderiam ser definidas pelo cubo dos… “números primos” maiores que 10…e etc. Com o auxílio desta numeração, Gödel construiu uma maneira única de associar um número a uma sentença matemática…a qual corresponderia um único nº – que…recuperado…seria transformado de volta na sentença que o originou.
A construção de um indecidível. Seguindo estes passos Gödel numera (‘nº de Gödel’) enunciados do tipo p -> q (provas matemáticas que podem ser lidas como “a fórmula p é a demonstração da fórmula q“). Esse novo número conterá…na sua decomposição única em ‘fatores primos‘ … as respectivas decomposições dos nºs referentes às fórmulas p e q separadamente, que poderão ser a seguir recuperados para a identificação de p e q, relacionados pelo símbolo -> de implicação…Se os nºs de Gödel das fórmulas p e q são x e y, respectivamente, podemos criar uma nova fórmula que traduz esta prova … que será simbolizada por Dem(x,y)…devendo ser lida do seguinte modo: o conjunto de fórmulas com nº de Gödel x é uma prova da fórmula cujo nº de Gödel é y. – A fórmula Dem (x,y) terá também seu número de Gödel, bem como ~Dem (x,y), que expressa que a fórmula, ou conjunto de fórmulas com nº de Gödel x…não é prova da fórmula com nº de Gödel y.
Agora a tentativa é a de reproduzir dentro da aritmética o paradoxo de Richard construindo uma sentença matemática ‘auto referente’ e ‘auto excludente’… mas, evitando as imprecisões nele contidas. – O que significa, construir um paradoxo na tentativa de provar que existe algo… — que não pode ser provado.
Provando o improvável “Fazer matemática parece descoberta. Se a estivéssemos inventando, certamente não seria tão difícil provar coisas — as quais… queremos desesperadamente, que sejam verdades…mas não são”. (Sarah Hart)
“A fórmula de número de Gödel y (identidade) não pode ser demonstrada”… que é o indecidível desejado. Observe que a fórmula que não pode ser demonstrada é…”que existe uma fórmula que não pode ser demonstrada“. E a isso se chama, uma recursividade!…A seguir analisaremos as conclusões da construção do indecidível:
1-Se a matemática é consistente, sua consistência não pode ser provada dentro da própria matemática. 2-Se a matemática é consistente ela é incompleta…(existem indecidíveis).
Interpretação dos resultados.
O que verificamos na sessão anterior tem consequências ‘impressionantes’ no que se refere, explicitamente, aos básicos fundamentos da matemática. Segundo o conceito de ‘consistência’: “Para a matemática ser ‘consistente‘, ela precisa se livrar de contradições”, isto é…dos “paradoxos internos”, caso contrário…será “inconsistente“.
Neste ponto precisamos definir o conceito de Completitude. Chamaremos um sistema de ‘completo’ se ele for capaz de provar ou contraprovar qualquer de suas afirmações, isto é, se ele for livre de indecidíveis. Caso contrário, o sistema será ‘incompleto’… Este sistema incompleto, no qual foi detetado um indecidível, pode ser parcialmente completado pela introdução…de fora para dentro, de um novo postulado para o sistema, capaz de decidir sobre a verdade ou falsidade do indecidível em questão…Tal sistema assim ampliado, se verá livre da mazela herdada pelo…surgimento do ‘indecidível’ – mas não estará livre do aparecimento de novos indecidíveis; e este é um ponto fundamental na ‘prova de Gödel‘.
Inicialmente…podemos observar que o que construímos foi uma fórmula que afirma de si mesmo… – “Eu não posso ser provado“, e que assim, tem a estrutura paradoxal de ser verdadeira se e somente se for falsa… Vejamos: se (x)~Dem(x,G(y)) for verdadeira, isto é, demonstrável dentro do sistema…como uma verdade desse sistema – como ela diz de si mesmo que não pode ser demonstrada, será falsa…mas se falsa – isto é… se não puder ser demonstrada como uma verdade dentro/do sistema, pelo princípio do 3º excluído, valerá a sua negação que atesta que ela pode sim, ser demonstrada, e que portanto, é verdadeira.
Estamos em pleno paradoxo, a não ser que o sistema se declare impotente quanto a decidir se a fórmula em questão é verdadeira ou falsa… – “Ou o paradoxo…ou o indecidível”.
1ª conclusão… “O preço da consistência é a incompletitude“.
Diante de tal ‘incompletitude’, isto é, expulso o paradoxo…transformado em indecidível, e que portanto não pode ser provado dentro do sistema, é possível, mesmo assim, a tomada de uma decisão…Usando ferramentas meta-sistemáticas poderemos ser capazes de julgar como verdadeiro ou falso a afirmação contida na ‘fórmula indecidível’…e, incluí-la dentro do sistema… – como verdadeira ou falsa… – por meio de um novo postulado, anexado ao sistema. Assim, através de sua “axiomatização”, nos livramos do fantasma do ‘indecidível’.

A matemática é cheia de exemplos deste tipo. O famoso “5º postulado de Euclides” da geometria plana, que afirma a unicidade das paralelas, foi … durante mais de dois mil anos…uma conjectura que deveria ser provada, através de uma geometria que somente utilizasse…os 4 primeiros postulados… – Com a eclosão das chamadas ‘geometrias não euclidianas’, numa das passagens mais belas da história da matemática…é comprovada a independência desse resultado… A conjectura se torna então um… “indecidível“… sendo consequentemente, reintroduzida na geometria — como o… ‘5º postulado‘.
Poderíamos nos sentir felizes, pela possibilidade de completamento da matemática…mas os resultados de Gödel não permitem nem essa alegria momentânea. Se analisarmos com calma… veremos que o surgimento do “indecidível” não depende do sistema considerado, desde que ele seja grande o suficiente para conter a aritmética. A introdução de um novo postulado não o “salva”, muito pelo contrário. Apenas sistemas pequenos poderiam estar livres – tanto de paradoxos como de indecidíveis, e estes sistemas não seriam capazes de investigar os estranhos caminhos do infinito, como faz a matemática…e a aritmética, em particular. Ao concluirmos o sistema, outros indecidíveis surgirão. – Eles são inevitáveis.
2ª conclusão… “se a matemática é consistente (livre de paradoxos)… — então ela é incompleta”. Em linguagem matemática esta afirmação pode ser traduzida como:
∃ y (x)~Dem(x,y) -> (x)~Dem(x,G(y)),
Já que a primeira parte afirma a consistência do sistema… – enquanto a segunda parte a existência do indecidível, que é equivalente à sua ‘incompletude’. Examinando a fórmula acima concluímos que se pudermos demonstrar a existência de pelo menos uma fórmula impossível de ser demonstrada – estaremos demonstrando também a fórmula específica que assegura a existência de um “indecidível“, que… como visto… é indemonstrável.
É a segunda conclusão dos teoremas de Gödel então que surge: “Sendo o sistema consistente…sua consistência não pode ser demonstrada neste sistema“.
Observe que, caso contrário, poderíamos demonstrar a fórmula ∃ y (x)~Dem(x,y) implicando na demonstração da fórmula (x)~Dem[xG(y)] que, como vimos, para se manter a consistência do sistema não pode ser nem provada nem contraprovada. Como as fórmulas acima referem-se a afirmações da metamatemática; mapeada dentro da aritmética pela numeração de Gödel – podemos finalmente concluir que: “Se o sistema matemático é consistente – sua consistência não pode ser provada nem por uma metamatemática mapeada de dentro do sistema“.
Mais precisamente, temos: “Se a aritmética é consistente, sua consistência não pode ser determinada…por qualquer argumento metamatemático que possa ser representado — dentro de um … formalismo aritmético“.
Esta conclusão surpreendente não anula – no entanto…a possibilidade de que algum argumento metamatemático, fora totalmente do sistema, possa provar a consistência da aritmética…O que temos é que o sistema em si, ou alguma extensão sua que possa ser nele mapeado — não é capaz de provar — a sua própria consistência. (texto base) ***************************(texto complementar)******************************
Riemann… e a Hipótese dos ‘Números primos’ “Inegavelmente a matemática é a única ‘linguagem universal’… – Podemos imaginar diferentes químicas ou biologias do outro lado do universo, mas os ‘números primos’ continuarão sendo primos … em qualquer galáxia que encontremos”. (Alain Connes)
Números primos, são aqueles apenas divisíveis por si próprios e pela unidade. Nenhum nº par…(“exceto 2″)…pode ser primo, porque todos os pares podem ser divididos por 2. – Mas, por exemplo, 3 é primo…assim como 19 também, porque não se pode dividi-los… — por qualquer outro número…além deles mesmos…e 1.
Já se sabe que os ‘números primos’ são infinitos e que existem alguns métodos para tentar localizá-los… – mas… além disso… há outros mistérios fascinantes.
Não existe até hoje alguma fórmula capaz de agrupar todos os números primos. Ainda é impossível prever…quando o próximo vai aparecer… – às vezes eles estão separados por mais de mil números…e outras vezes – por um número apenas – e esses são conhecidos como ‘números primos gêmeos‘. Mas sabemos que a distribuição dos primos, apesar de parecer aleatória, não o é… – o que acontece é que ainda não conseguimos ver qualquer harmonia nela. (E isso é muito misterioso!…) É incrível que ainda seja impossível de se encontrar um padrão para a localização deles, ainda mais se pararmos para pensar que esses números são os ‘blocos de construção‘ para qualquer outro número… – já que todo e qualquer número pode ser gerado a partir da multiplicação dos números primos.
A Hipótese de Riemann
Em 1859, o matemático Bernard Riemann fez uma ‘hipótese’ — que continua sendo o principal avanço em direção a uma ordem no caótico mundo dos… ‘números primos’. Basicamente… a ‘hipótese de Riemann’ diz que existe uma fórmula na ‘função zeta’ de Riemann…definida num gráfico 4D – com base nos números naturais, e imaginários, onde todos zeros “não-triviais” (formados por nºs naturais positivos), se agrupariam sempre, sobre a mesma linha … conectada com a localização dos… “números primos”.
O problema é que até agora ninguém conseguiu provar a hipótese de Riemann, principalmente porque os zeros, assim como os números primos, são infinitos; e, temos que achar cada zero, um por um…Até agora já foram encontrados 6,3 bilhões de zeros sobre a linha, e nenhum fora dela. Mesmo assim, ainda não é possível garantir que a hipótese seja verdadeira… – Sem um modo de prever a localização de todos os zeros é impossível provar que estejam na mesma linha.
A harmonia por trás do distribuição dos números primos continua sendo… — um dos maiores ‘mistérios’ do mundo.
Mas, talvez a prova da “hipótese de Riemann” seja tão intrincada…que o cérebro humano não consiga alcançá-la. E assim, a lógica por trás dos números primos estaria mesmo fora do nosso alcance, comprovando então o ‘teorema da incompletude‘ de Gödel, que diz que existem certas teorias, que mesmo verdadeiras, jamais poderão ser provadas. Essa é uma perspectiva triste. Mas talvez a beleza desses números, venha justamente da sua natureza egoísta, em que cada um existe totalmente sozinho – sem divisor, e sem previsão de onde estará o próximo – que pudesse compor uma paisagem maior que si próprio. (texto base) ***********************************************************************************
“Teoria Analítica dos Números (Primos)” A invenção do Cálculo Diferencial e Integral provocou um dos maiores avanços no ‘pensamento ocidental’…O trabalho monumental de Newton e Leibniz propiciou o avanço da ciência em todas suas áreas. O matemático Leonhard Euler (1707/1783) foi um dos pioneiros a usar métodos do Cálculo à ‘Teoria (Analítica) dos Números’. Contudo, o reconhecimento de tal feito…foi para Bernard Riemann (1826/1866).
Riemann revolucionou a Análise Matemática, a Geometria e a Física Matemática. Em Teoria Analítica dos Números, bem como em outras áreas da Matemática, suas ideias ainda exercem profunda influência. Variedades Riemannianas, Equações de Cauchy– Riemann, Superfícies de Riemann, e muitos outros assuntos encontram-se entre seus trabalhos. – Mas, um fato peculiar, é que a chave para alguns dos maiores problemas contemporâneos reside em uma conjectura sua, denominada “Hipótese de Riemann”:
 Tudo começou quando Euler definiu em 1740 uma função – denotada pela letra grega ζ (“zeta”)… – A “função zeta“ de Euler, associa a todo número real maior que 1 … um outro diferente — “número real”.
Tudo começou quando Euler definiu em 1740 uma função – denotada pela letra grega ζ (“zeta”)… – A “função zeta“ de Euler, associa a todo número real maior que 1 … um outro diferente — “número real”.
É interessante notar, que ao encontrar a relação ζ (2) = π2/6… Euler observou que essa função daria informações sobre o padrão dos números primos. Nascia assim, a Teoria Analítica dos Números, ou seja, o estudo dos ‘números primos’…através do Cálculo aplicado à investigação de propriedades de algumas ‘funções complexas‘. Apesar de não se visualizar um gráfico dessas funções (com dimensão 4)…é possível, com a ajuda de um bom software… – definir as partes “real“…e “imaginária” de uma tal função.
Convém observar que existem inúmeras funções zeta e alguns matemáticos costumam dizer que Teoria dos Números é o estudo de funções zeta. Porém, qual é a relação entre os “números primos” e a “função zeta” de Euler?
 “Função Zeta” dos Números primos
“Função Zeta” dos Números primos
Euler demonstrou um impressionante teorema… afirmando que para qualquer número real maior que 1…a “função zeta” se expressa como produto infinito de fatores para qualquer ‘número primo’. Tal função…foi minuciosamente investigada por Riemann ao substituir o número real (x) por um ‘número complexo‘, forma algébrica (z = a + bi); o que tornou a “função zeta” do tipo “complexa”.
Tal função não está definida para todos números complexos. Porém, Riemann percebeu que com uma técnica da “Teoria das Funções Complexas” seria possível estendê-la para todos os ‘complexos’, exceto para o número z = 1. – Em 1859, publicou seu fundamental artigo, usando a ‘função zeta’ para checar o padrão dos “números primos”…Seu objetivo era demonstrar a Conjectura de Gauss, hoje mais conhecida como ‘Teorema do Número Primo’, provando que a quantidade de números de primos entre (1 e x)…para grandes x, é aproximadamente o próprio x, dividido pelo logaritmo natural de x, isto é…(x / ln x).
Embora Riemann não tivesse obtido sucesso…seu trabalho foi de suma importância para o desenvolvimento da “Teoria Analítica dos Números“. Vários resultados foram obtidos quando da investigação das propriedades dessa função, intimamente ligadas à distribuição de números primos, ao longo de sua sequência natural no conjunto dos ‘inteiros positivos’.
O caminho de futuros progressos investigativos ficou assim esquematizado…em uma série de conjecturas bem fundamentadas…dentre as quais, a famosa “Hipótese de Riemann”.
Em 1896, os matemáticos… J. Hadamard e De la Vallée-Poussin, demonstraram, independentemente…o “Teorema do Número Primo“…utilizando as ideias então desenvolvidas por Riemann.
Consideremos a equação ζ(s) = 0. Então, qualquer número complexo s, que resolva essa equação é denominado um “zero” da equação. Riemann observou primeiramente, que os inteiros negativos pares –2, -4 –6… são zeros da função…Depois, observou que deveriam existir infinitos zeros complexos, e então estabeleceu de forma audaciosa a conjectura de que…qualquer outro zero complexo da função zeta — possui parte real igual a ½, ou seja, tem a forma (s = ½ + b i). Portanto, todos os zeros da função zeta que não são números reais estarão na reta vertical (x = ½). Essa reta é geralmente chamada de “reta crítica“.
A primeira coisa a observar é que os zeros da reta crítica não são reais, colocam-se simetricamente em relação ao eixo real e também em relação à própria reta crítica. Essa é a célebre “hipótese de Riemann“…sem dúvida, uma questão importante, pois o arranjo dos zeros da função zeta – se traduz na distribuição dos nºs primos.
A ‘Hipótese de Riemann’ foi considerada um dos problemas do milênio, pois é o problema mais importante da Matemática ainda não resolvido… — com algumas consequências em Física quântica … e, profundas repercussões na Teoria da Informação, em especial, na questão de “segurança”. (texto base) ***********************************************************************
Física explica enigma da Matemática, a Hipótese de Riemann (nov/2021) O fato da matemática fornecer à física a linguagem certa para formular as leis da natureza está na própria lógica das coisas. Porém, a possibilidade da física fornecer a ‘chave’ para a compreensão de um genuíno mistério da matemática — ao contrário… é um fato bastante incomum e extraordinário. Mas é o que agora parece estar acontecendo pela primeira vez.

A Física precisa da Matemática para quase tudo – mas ninguém imaginava que o contrário também poderia ser verdadeiro. [Sissa]
No cerne do argumento de Riemann havia uma conjectura que ele não foi capaz de provar, sobre a localização de um nº infinito de zeros – no “plano complexo” de uma certa função, conhecida como “função de Riemann“…Esses zeros parecem se alinhar “magicamente” ao longo de uma linha vertical com uma abscissa exatamente igual a 1/2…Até agora ninguém conseguiu entender a razão de uma regularidade tão incrível. Mas Giuseppe Mussardo, da “Escola Internacional de Estudos Avançados” — Itália, e seu colega André Leclair acabam de demonstrar uma explicação extremamente elegante para tal alinhamento dos zeros, ao longo do eixo 1/2 da ‘função de Riemann‘, bem como de infinitas funções semelhantes: as chamadas…”funções de Dirichlet”. – Segundo eles, em última análise, essa distribuição se deve à surpreendente presença de um “movimento caótico” e suas “leis de probabilidade”.
Na verdade, numa espécie de reciprocidade…ou simetria no conhecimento, eles provaram a existência de um movimento browniano, oculto por trás de todas essas funções infinitas: Há pouco tempo, físicos mostraram que a função de onda, que explica partículas atômicas e subatômicas, é uma matemática que virou realidade…Agora, os matemáticos mostraram que um movimento aleatório das partículas explica a presença de um ‘padrão matemático’.
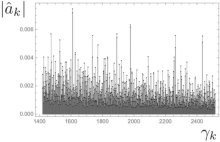
A estatística do movimento browniano explica os infinitos zeros na plotagem dos números primos. [Imagem: Giuseppe Mussardo et al.]
O “movimento browniano”, explicado pela 1ª vez por Einstein em 1906 – e ‘fenômeno-chave‘ na mecânica estatística, é o movimento caótico dos átomos de um gás – devido à ‘altíssima frequência’ de suas colisões. Nele, o expoente universal que rege como os átomos se espalham ao longo do tempo (1/2), se deve às leis probabilísticas de Gauss, como parte do seu famoso: “teorema do limite central“: “Quando o tamanho de uma amostra aumenta — sua ‘distribuição média‘ se aproxima de uma distribuição normal … gaussiana”.
Segundo Mussardo: “Nossa hipótese sobre a natureza browniana da conjectura de Riemann…amparada numa série de resultados probabilísticos – que provamos na “Teoria dos Números”…se fez acompanhar por uma ‘análise estatística‘ robusta, e extremamente precisa – realizada ao longo da sequência infinita de…’nºs primos’, uma verdadeiro façanha que nos manteve ocupados por cerca de três anos. O fato da explicação da conjectura de Riemann vir da física (mecânica estatística)…e, as surpreendentes conexões desse campo…com um tema genuinamente matemático, como a ‘teoria dos números’ – revela também a grande unidade do conhecimento científico – bem como…aumenta nosso espanto…diante de um fato tão profundo”. Matemáticos e físicos poderão se “deleitar” com este trabalho…mas suas maiores implicações, provavelmente ficarão por conta da ‘filosofia da ciência’. (texto base)










CurtirCurtir